题目内容
函数y=|2x-1|的大致图象是（ ）
A、 |
B、 |
C、 |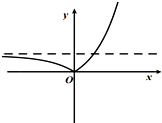
D、 |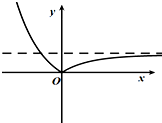
考点：指数函数的图像变换
专题：函数的性质及应用
分析：先将函数的绝对值符号去掉，化成分段函数，再分别判断其图象形状，则问题容易解决．
解答：
解：y=|2x-1|=
，
当x＜0时，y=1-2x的图象是将y=2x图象先沿x轴对称下来，再沿y轴向上平移1个单位，此时x＜0时的图象在x轴上方，且为增函数，渐近线为y=1，
只有C项满足题意．
故选C
|
当x＜0时，y=1-2x的图象是将y=2x图象先沿x轴对称下来，再沿y轴向上平移1个单位，此时x＜0时的图象在x轴上方，且为增函数，渐近线为y=1，
只有C项满足题意．
故选C
点评：这是一道考查函数图象的问题，本题的思路是先将绝对值符号去掉，转化成基本初等函数，再抓住x＜0时四个选择支图象不同，专门判断y=1-2x的图象完成解答．当然还可先画出y=2x-1的图象，利用图象变换的方法直接得到所求的函数图象，再进行选择．
练习册系列答案
相关题目
设复数z满足（z+i）（1+i）=1-i（i是虚数单位），则|z|=（ ）
| A、1 | B、2 | C、3 | D、4 |
i是虚数单位，则复数
的虚部为（ ）
| 2i |
| 1-i |
| A、-i | B、-1 | C、1 | D、i |
已知实数x，y满足
，若z=y-ax取得最大值时的唯一最优解是（3，2），则实数a的取值范围为（ ）
|
| A、a＜1 | B、a＜2 |
| C、a＞1 | D、0＜a＜1 |
已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，-
＜φ＜
），其部分图象如图所示，将f（x）的图象纵坐标不变，横坐标变成原来的2倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）
| π |
| 2 |
| π |
| 2 |
A、g（x）=sin
| ||
B、g（x）=sin
| ||
C、g（x）=sin（
| ||
D、g（x）=sin（
|
圆（x-1）2+（y+2）2=5的圆心坐标为（ ）
| A、（1，2） |
| B、（1，-2） |
| C、（-1，2） |
| D、（-1，-2） |
用反证法证明命题“三角形的内角中至多有一个钝角”时，假设正确的是（ ）
| A、三个内角中至少有一个钝角 |
| B、三个内角中至少有两个钝角 |
| C、三个内角都不是钝角 |
| D、三个内角都不是钝角或至少有两个钝角 |
| sinα+cosα |
| sinα-cosα |
A、-
| ||
B、
| ||
C、-
| ||
D、
|