题目内容
1．
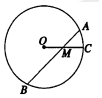圆内两条相交弦长，其中一弦长为8cm，且被交点平分，另一条弦被交点分成1：4两部分，则这条弦长是（ ）| A． | 2cm | B． | 8cm | C． | 10cm | D． | 12cm |
分析 设另一条弦分成的两段AM=x，BM=4x，由相交弦定理，代入求出即可．
解答 解：设另一条弦分成的两段AM=x，BM=4x，
由题意由相交弦定理得：AP×BP=CP×DP，
则4×4=x•4x，
x=2，
则AB=x+4x=10（cm），
故选：C．
点评 本题考查了相交弦定理和解一元二次方程，比较基础．
练习册系列答案
相关题目
16．圆心在x轴上，半径为1，且过点（2，1）的圆的方程是（ ）
| A． | （x-2）2+y2=1 | B． | （x+2）2+y2=1 | C． | （x-1）2+（y-3）2=1 | D． | x2+（y-2）2=1 |
6．直线x+y+1=0关于点（1，2）对称的直线方程为（ ）
| A． | x+y-7=0 | B． | x-y+7=0 | C． | x+y+6=0 | D． | x-y-6=0 |
10．若直线ax-by+1=0（a＞0，b＞0）分圆C：x2+y2+2x-4y+1=0的周长，则ab的取值范围是（ ）
| A． | （-∞，$\frac{1}{8}$] | B． | （0，$\frac{1}{8}$] | C． | （0，$\frac{1}{4}$] | D． | [$\frac{1}{4}$，+∞） |