题目内容
12.已知△ABC中.AB=BC,延长CB至D,使AC⊥AD,若$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ-μ=3.分析 根据题意画出图形,结合图形得出AB是Rt△ACD斜边的中线,用向量$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{AD}$,求出λ、μ的值即可.
解答 解:如图所示,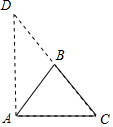
△ABC中,AB=BC,
延长CB到D,使AC⊥AD,
∴AB是Rt△ACD的斜边CD上的中线,
∴$\overrightarrow{AB}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AD}$),
化为$\overrightarrow{AD}$=2$\overrightarrow{AB}$-$\overrightarrow{AC}$.
与$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$比较,
得λ=2、μ=-1,
∴λ-μ=3.
故答案为:3.
点评 本题考查了直角三角形斜边中线的性质与向量的线性运算问题,是基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
2.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)以椭圆C2:$\frac{{x}^{2}}{{m}^{2}}+\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)的焦点F1,F2为顶点,且以椭圆C2的右顶点A为一个焦点,它的一条渐近线与椭圆C2交于P,Q,若$\overrightarrow{AP}•\overrightarrow{PQ}$=0,则双曲线C1的离心率e满足( )
| A. | e2=$\frac{\sqrt{2}+1}{2}$ | B. | e2=$\frac{\sqrt{3}+1}{2}$ | C. | e2=$\frac{3}{2}$ | D. | e2=$\frac{\sqrt{5}+1}{2}$ |
3.与直线y=2x平行的抛物线y=x2的切线方程是( )
| A. | 2x-y+3=0 | B. | 2x-y-3=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
1.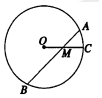 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |