题目内容
13.对于定义在R上的奇函数f(x),满足f(x+3)=f(x),若f(-1)=1,则f(1)+f(2)+…+f(10)=-1.分析 根据函数是一个奇函数先求出f(1),根据函数满足f(x+3)=f(x),得到函数是一个周期函数,利用周期性和奇函数得到要求的结果.
解答 解:∵f(x)是奇函数,∴f(-x)=-f(x)
所以f(1)=-f(-1)=-1
f(2)=f((-1)+3)=f(-1)=1
∵f(0)=f(3)=-f(-3)=-f(-3+3)=-f(0)
所以f(0)=0
而f(10)=f(7)=f(4)=f(1)
f(9)=f(6)=f(3)=f(0)
f(8)=f(5)=f(2)
∴f(1)+f(2)+…+f(10)
=4f(1)+3f(2)+3f(0)
=-4+3=-1
故答案为-1.
点评 本题考查函数的奇偶性和函数的周期性,本题解题的关键是看出在要求的十个变量的函数值中,可以分成三部分,分别求出结果.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
3.与直线y=2x平行的抛物线y=x2的切线方程是( )
| A. | 2x-y+3=0 | B. | 2x-y-3=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
1.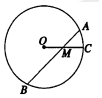 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
8.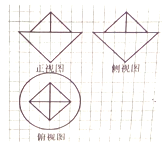 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$ | B. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$-8 | C. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$ | D. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$-8 |
18.若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)•f(x-1)定义域为( )
| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
5.经过点(-1,1),斜率是直线y=$\frac{\sqrt{2}}{2}$x-2的斜率的2倍的直线方程是( )
| A. | x=-1 | B. | y=1 | C. | y-1=$\sqrt{2}$(x+1) | D. | y-1=2$\sqrt{2}$(x+1) |
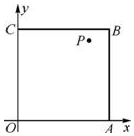 如图,在边长为1的正方形OABC内任取一点P(x,y).
如图,在边长为1的正方形OABC内任取一点P(x,y).