题目内容
9.函数f(x)=cos(x+2θ)+2sinθsin(x+θ)的最小值为-1.分析 利用两角和与差的余弦公式,对f(x)化简,再根据余弦函数的图象与性质得出函数f(x)的最小值.
解答 解:f(x)=cos(x+2θ)+2sinθsin(x+θ)
=cos(x+θ)cosθ-sin(x+θ)sinθ+2sinθsin(x+θ)
=cos(x+θ)cosθ+sin(x+θ)sinθ
=cos(x+θ-θ)
=cosx,
根据余弦函数的图象与性质得函数f(x)的最小值为-1.
故答案为:-1.
点评 本题考查了两角和与差的余弦公式以及余弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列命题中,为真命题的是( )
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | |
| B. | $sinx+\frac{1}{sinx}≥2(x≠kπ,k∈Z)$ | |
| C. | ?x∈R,2x>x2 | |
| D. | 若命题p:?x0∈R,使得$x_0^2-{x_0}+1<0$,则¬p:?x0∈R,都有x2-x+1≥0 |
1.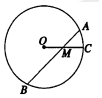 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
18.若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)•f(x-1)定义域为( )
| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
 为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.
为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.