题目内容
11.将图形C上的动点的坐标所组成的向量$(\begin{array}{l}{x}\\{y}\end{array})$左乘矩阵$(\begin{array}{l}{0}&{1}\\{1}&{0}\end{array})$,得到新的动点所构成的图形与图形C的位置关系为关于直线y=x对称.分析 将图形C上的动点的坐标所组成的向量$(\begin{array}{l}{x}\\{y}\end{array})$左乘矩阵($(\begin{array}{l}{0}&{1}\\{1}&{0}\end{array})$,得到新的动点的坐标组成的向量为$(\begin{array}{l}{y}\\{x}\end{array})$.由此能求出结果.
解答 解:$(\begin{array}{l}{0}&{1}\\{1}&{0}\end{array})$$(\begin{array}{l}{x}\\{y}\end{array})$=$(\begin{array}{l}{y}\\{x}\end{array})$.
∴将图形C上的动点的坐标所组成的向量$(\begin{array}{l}{x}\\{y}\end{array})$左乘矩阵$(\begin{array}{l}{0}&{1}\\{1}&{0}\end{array})$,
得到新的动点所构成的图形与图形C的位置关系为关于直线y=x对称.
故答案为:关于直线y=x对称.
点评 本题考查两动点图形的位置关系的判断,是基础题,解题时要认真审题,注意矩阵乘法的性质的合理运用.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
13.已知函数f(x)=3sin(3x+φ),x∈[0,π],则y=f(x)的图象与直线y=2的交点个数最多有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)以椭圆C2:$\frac{{x}^{2}}{{m}^{2}}+\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)的焦点F1,F2为顶点,且以椭圆C2的右顶点A为一个焦点,它的一条渐近线与椭圆C2交于P,Q,若$\overrightarrow{AP}•\overrightarrow{PQ}$=0,则双曲线C1的离心率e满足( )
| A. | e2=$\frac{\sqrt{2}+1}{2}$ | B. | e2=$\frac{\sqrt{3}+1}{2}$ | C. | e2=$\frac{3}{2}$ | D. | e2=$\frac{\sqrt{5}+1}{2}$ |
3.与直线y=2x平行的抛物线y=x2的切线方程是( )
| A. | 2x-y+3=0 | B. | 2x-y-3=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
1.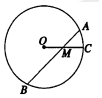 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
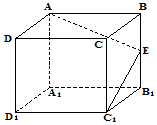 如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )