题目内容
11．已知O是坐标原点，点A（-1，1），若点M（x，y）为平面区域$\left\{\begin{array}{l}x+y≥2\\ x≤1\\ y≤2\end{array}\right.$上的一个动点，则 $\overrightarrow{OA}•\overrightarrow{OM}$的最大值是2．分析 作出不等式组对应的平面区域，结合向量数量积的公式，将结论进行转化，利用数形结合进行求解即可．
解答 解：作出不等式组对应的平面区域如图：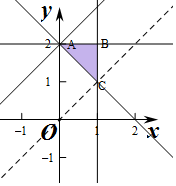
则 $\overrightarrow{OA}•\overrightarrow{OM}$=-x+y，
设z=-x+y，则y=x+z，
平移直线y=x+z，当直线y=x+z经过点A时，直线y=x+z的截距最大，此时z最大，
由$\left\{\begin{array}{l}{y=2}\\{x+y=2}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$，得A（0，2），
此时z=-0+2=2，
故 $\overrightarrow{OA}•\overrightarrow{OM}$的最大值是2，
故答案为：2．
点评 本题主要考查线性规划的应用，结合向量数量积的公式结合数形结合是解决本题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
1．
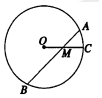圆内两条相交弦长，其中一弦长为8cm，且被交点平分，另一条弦被交点分成1：4两部分，则这条弦长是（ ）
圆内两条相交弦长，其中一弦长为8cm，且被交点平分，另一条弦被交点分成1：4两部分，则这条弦长是（ ）| A． | 2cm | B． | 8cm | C． | 10cm | D． | 12cm |
为美化环境，某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂（如图所示）．已知A、B两地的距离为10km，垃圾场对某地的影响度与其到该地的距离关，对A、B两地的总影响度为对A地的影响度和对B地影响度的和．记C点到A地的距离为xkm，垃圾处理厂对A、B两地的总影响度为y．统计调查表明：垃圾处理厂对A地的影响度与其到A地距离的平方成反比，比例系数为$\frac{3}{2}$；对B地的影响度与其到B地的距离的平方成反比，比例系数为k．当垃圾处理厂建在弧$\widehat{AB}$的中点时，对A、B两地的总影响度为0.15．
6．函数f（x）在定义域R内可导，f（x）=f（2-x），当x∈（1，+∞）时，（x-1）f′（x）＜0，设a=f（log32），b=f（log52），c=f（log25），则（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | a＜b＜c | D． | b＜a＜c |
16．设函数f（x）和g（x）分别是R上的偶函数和奇函数，则下列结论恒成立的是（ ）
| A． | f（x）•|g（x）|是奇函数 | B． | f（x）+|g（x）|是偶函数 | C． | |f（x）|-g（x）是奇函数 | D． | |f（x）|•g（x）是偶函数 |
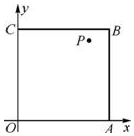如图，在边长为1的正方形OABC内任取一点P（x，y）．