题目内容
在区间[-1，3]是任取实数a，使得关于x的方程x2-2x+a=0有实根的概率为 ．
考点：几何概型
专题：概率与统计
分析：根据几何概型计算公式，首先求出方程有实根的a的范围，然后用符合题意的基本事件对应的区间长度除以所有基本事件对应的区间长度，即可得到所求的概率．
解答：
解：∵方程x2-2x+a=0有实根，
∴4-4a≥0，
∴a≤1时方程有实根，
∵在区间[-1，3]上任取一实数a，区间长度为4，[-1，1]的区间长度为2，
∴所求的概率为P=
=0.5；
故答案为：0.5．
∴4-4a≥0，
∴a≤1时方程有实根，
∵在区间[-1，3]上任取一实数a，区间长度为4，[-1，1]的区间长度为2，
∴所求的概率为P=
| 2 |
| 4 |
故答案为：0.5．
点评：本题着重考查了几何概型计算公式及其应用的知识，给出在区间上取数的事件，求相应的概率值．关键是明确事件对应的是区间长度或者是面积或者体积．
练习册系列答案
相关题目
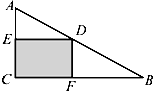在RT△ABC中，直角边AC=3，BC=4，点D是斜边AB上的动点，DE⊥AC交AC于点E，DF⊥BC交BC于点F，设CE=x．若点P（m，n）Q（n-1，m+1）关于直线l对称，则l的方程是（ ）
| A、x-y+1=0 |
| B、x-y=0 |
| C、x+y+1=0 |
| D、x+y=0 |