Question

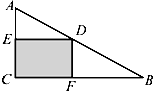在RT△ABC中，直角边AC=3，BC=4，点D是斜边AB上的动点，DE⊥AC交AC于点E，DF⊥BC交BC于点F，设CE=x．
（Ⅰ）求四边形FDEC的面积函数f（x）；
（Ⅱ）当x为何值时，f（x）最大？并求出f（x）的最大值．

Answer 1

考点：基本不等式在最值问题中的应用

专题：不等式的解法及应用

分析：（1）根据图形得出

AE

AC

=

EF

BC

，求解得四边形FDEC的面积函数f（x）=x（4-

4x

3

），0＜x＜3，
（2）利用基本不等式x（4-

4x

3

）=12×

x

3

×（1-

x

3

）≤12×

1

4

=3，0＜x＜3，求解即可．

解答： 解：（1）设设CE=x．则AE=3-x，
∵

AE

AC

=

EF

BC

，
∴EF=4-

4x

3

，0＜x＜3，
∴四边形FDEC的面积函数f（x）=x（4-

4x

3

），0＜x＜3，
（2）∵f（x）=x（4-

4x

3

）=12×

x

3

×（1-

x

3

）≤12×

1

4

=3，0＜x＜3，
∴当

x

3

=1-

x

3

时，即x=

3

2

时，等号成立．
∴当x=

3

2

时，f（x）最大=3．

点评：本题考查了函数在实际问题中的应用，利用基本不等式求解最值问题，属于中档题．