题目内容
在△ABC中，已知a=6，b=4，C=120°，则c的值是（ ）
| A、76 | ||
B、2
| ||
| C、28 | ||
D、2
|
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，将a，b，cosC的值代入计算即可求出c的值．
解答：
解：∵在△ABC中，a=6，b=4，C=120°，
∴由余弦定理得：c2=a2+b2-2abcosC=36+16+24=76，
则c=2
．
故选：B．
∴由余弦定理得：c2=a2+b2-2abcosC=36+16+24=76，
则c=2
| 19 |
故选：B．
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
观察圆周上n个点之间所连成的弦，发现2个点可以连成一条弦，3个点可以连成3条弦，4个点可以连成6条弦，5个点可以连成10条弦，由此可以推广到n∈N*的规律是（ ）
| A、6个点可以连成15条弦 | ||
B、n个点可以连成
| ||
C、n个点可以连成
| ||
| D、以上都不对 |
设函数f（x）=lnx+1可导，则
等于（ ）
| lim |
| △x→0 |
| f(1+3△x)-f(1) |
| △x |
| A、1 | ||
| B、0 | ||
| C、3 | ||
D、
|
在等差数列{an}中，若a3+a5+a7+a9+a11=100，则a2+a12的值为（ ）
| A、20 | B、30 | C、40 | D、50 |
已知一个正方体的8个顶点都在同一个球面上，则球的表面积与这个正方体的全面积之比为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
i为虚数单位，则z=1+i+i2+…+i10的共轭复数
等于（ ）
. |
| z |
| A、1-i | B、-i |
| C、-1+i | D、i |
若{an}为等差数列，Sn为其前n项和，且a5+a6+a7=48，则S11的值是（ ）
| A、176 | B、96 |
| C、256 | D、196 |
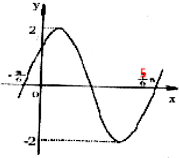如图，已知函数y=Asin（ωx+φ）（A＞0，0＜φ＜π）的图象经过点（-