题目内容
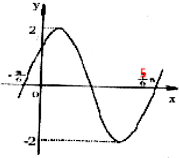如图，已知函数y=Asin（ωx+φ）（A＞0，0＜φ＜π）的图象经过点（-| π |
| 6 |
| 5 |
| 6 |
（1）求函数的解析式；
（2）求函数的增区间．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的单调性
专题：三角函数的图像与性质
分析：（1）由图可直接求得A，T，利用周期公式求ω，利用五点作图的第一点求φ；
（2）直接由复合函数的单调性求解函数的增区间．
（2）直接由复合函数的单调性求解函数的增区间．
解答：
解：（1）由图可知，A=2，T=
=
-(-
)=π，
∴ω=2．
由五点作图的第一点知，2×（-
）+φ=0，解得φ=
．
∴y=2sin（2x+
）；
（2）y=2sin（2x+
）．
由-
+2kπ≤2x+
≤
+2kπ，得
-
+kπ≤x≤
+kπ，k∈Z．
∴函数的单调增区间为[-
+kπ，
+kπ]，k∈Z．
| 2π |
| ω |
| 5π |
| 6 |
| π |
| 6 |
∴ω=2．
由五点作图的第一点知，2×（-
| π |
| 6 |
| π |
| 3 |
∴y=2sin（2x+
| π |
| 3 |
（2）y=2sin（2x+
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
-
| 5π |
| 12 |
| π |
| 12 |
∴函数的单调增区间为[-
| 5π |
| 12 |
| π |
| 12 |
点评：本题考查了由y=Asin（ωx+φ）的部分图象求函数解析式，考查了复合函数的单调性的求法，是中档题．
练习册系列答案
相关题目
在△ABC中，已知a=6，b=4，C=120°，则c的值是（ ）
| A、76 | ||
B、2
| ||
| C、28 | ||
D、2
|
函数f（x）=loga|x+1|，当x∈（-1，0）时，恒有f（x）＞0，有（ ）
| A、f（x）在（-∞，-1）上是增函数 |
| B、f（x）在（-∞，0）上是减函数 |
| C、f（x）在（0，+∞）上是增函数 |
| D、f（x）在（-∞，+∞）上是减函数 |