题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,若bcosA+acosB=-2ccosC.
(1)求角C的大小;
(2)若b=2a,且△ABC的面积为2
,求边c的长.
(1)求角C的大小;
(2)若b=2a,且△ABC的面积为2
| 3 |
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(1)由已知及正弦定理可得:sinBcosA+sinAcosB=-2sinCcosC,化简可得cosC=-
,从而可求C的值;
(2)由已知可得
a•2a•
=2
,从而可解得a,b的值,从而由余弦定理可解得c的值.
| 1 |
| 2 |
(2)由已知可得
| 1 |
| 2 |
| ||
| 2 |
| 3 |
解答:
解:(1)由bcosA+acosB=-2ccosC及正弦定理可得sinBcosA+sinAcosB=-2sinCcosC,
即sin(A+B)=-2sinCcosC,由A,B,C是三角形内角可知sin(A+B)=sinC≠0,
∴cosC=-
,
故C=
.
(2)由△ABC的面积可得
absinC=2
,即
a•2a•
=2
,
∴a=2,
∴b=4,
由余弦定理可得:c2=a2+b2-2abcosC=4+16-2×2×4×(-
)=28,
∴c=2
.
即sin(A+B)=-2sinCcosC,由A,B,C是三角形内角可知sin(A+B)=sinC≠0,
∴cosC=-
| 1 |
| 2 |
故C=
| 2π |
| 3 |
(2)由△ABC的面积可得
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴a=2,
∴b=4,
由余弦定理可得:c2=a2+b2-2abcosC=4+16-2×2×4×(-
| 1 |
| 2 |
∴c=2
| 7 |
点评:本题主要考察了正弦定理、余弦定理、三角形面积公式的应用,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
在平面直角坐标系中,曲线经过旋转或平移所产生的新双曲线与原双曲线具有相同的离心率和焦距,称它们为一组“任性双曲线”;例如将等轴双曲线x2-y2=2绕原点逆时针转动45°,就会得到它的一条“任性双曲线”y=
;根据以上材料可推理得出双曲线y=
的焦距为( )
| 1 |
| x |
| 3x+1 |
| x-1 |
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
设定点F1(0,-3)、F2(0,3)动点P满足条件|PF1|-a=
-|PF2|(a>0)则点P的轨迹是( )
| 9 |
| a |
| A、椭圆 | B、线段 |
| C、不存在 | D、椭圆或线段 |
下列运算正确的是( )
| A、(ax2-bx+c)′=a(x2)′+b(-x)′ |
| B、(cosx•sinx)′=(sinx)′•cosx+(cosx)′•cosx |
| C、(sinx-2x2)′=(sinx)′-(2)′(x2)′ |
| D、[(3+x2)(2-x3)]′=2x(2-x3)+3x2(3+x2) |
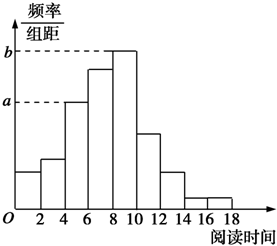 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图: 如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O,E是AB边的中点,EO的延长线交CD于F.
如图,在等腰梯形ABCD中,对角线AC⊥BD,且相交于点O,E是AB边的中点,EO的延长线交CD于F.