题目内容
在平面直角坐标系中，曲线经过旋转或平移所产生的新双曲线与原双曲线具有相同的离心率和焦距，称它们为一组“任性双曲线”；例如将等轴双曲线x2-y2=2绕原点逆时针转动45°，就会得到它的一条“任性双曲线”y=
；根据以上材料可推理得出双曲线y=
的焦距为（ ）
| 1 |
| x |
| 3x+1 |
| x-1 |
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程,推理和证明
分析：双曲线y=y=3+
的图象与双曲线y=
的图象全等，它们的焦距相同，又根据题意得：将双曲线x2-y2=8绕原点逆时针旋转45°后可得到双曲线y=
，故只须求出双曲线x2-y2=8的焦距即可．
| 4 |
| x-1 |
| 4 |
| x |
| 4 |
| x |
解答：
解：双曲线y=
即为y=3+
，
而双曲线y=3+
的图象可由y=
进行形状不变的变换而得，
∴双曲线y═3+
的图象与双曲线y=
的图象全等，它们的焦距相同，
根据题意：“将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y=
”
类比可得：将双曲线x2-y2=8绕原点逆时针旋转45°后可得到双曲线y=
，
而双曲线x2-y2=8的a=b=2
，c=
=8，
∴焦距为2c=8．
故选C．
| 3x+1 |
| x-1 |
| 4 |
| x-1 |
而双曲线y=3+
| 4 |
| x-1 |
| 4 |
| x |
∴双曲线y═3+
| 4 |
| x-1 |
| 4 |
| x |
根据题意：“将双曲线x2-y2=2绕原点逆时针旋转45°后可得到双曲线y=
| 1 |
| x |
类比可得：将双曲线x2-y2=8绕原点逆时针旋转45°后可得到双曲线y=
| 4 |
| x |
而双曲线x2-y2=8的a=b=2
| 2 |
| a2+b2 |
∴焦距为2c=8．
故选C．
点评：本题主要考查旋转变换、双曲线的简单性质等基础知识，考查运算求解能力，考查分析问题和解决问题的能力．属于中档题．
练习册系列答案
相关题目
执行如图所示的程序框图，输出的S值为 （ ）
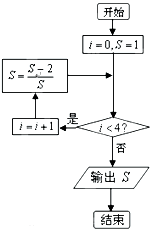
| A、-1 | ||
| B、3 | ||
C、
| ||
| D、-5 |
当参数θ变化时，动点P（2cosθ，3sinθ）所确定的曲线为（ ）
| A、直线 | B、圆 | C、椭圆 | D、双曲线 |
若曲线y=x2+ax+b在点（0，b）处的切线方程是y=x+1，则（ ）
| A、a=1，b=1 |
| B、a=-1，b=1 |
| C、a=1，b=-1 |
| D、a=-1，b=-1 |