题目内容
函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图,其中M(m,0),N(n,2),P(π,0),且mn<0,则f(x)在下列哪个区间中是单调的( )


A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:由题意得到三角函数的周期满足π<T<
,然后取周期接近π和接近
分别排除选项D、A、C,从而得到正确选项.
| 4π |
| 3 |
| 4π |
| 3 |
解答:
解:∵mn<0,
∴m,n异号,
由图可知:m<0,n>0.
又P(π,0),
∴T>π且
<π,
则π<T<
.
当周期无限接近π时,图中的最低点自左向右无限接近
,
∴f(x)在(
,π)上先减后增不单调,排除D;
当周期接近
又小于
时,图中最高点N的横坐标大于0小于
,
f(x)在(0,
)上先增后减不单调,排除A;
图中的最低点的横坐标大于
小于
,f(x)在(
,
)上先减后增不单调,排除C.
∴正确的答案为B.
故选:B.
∴m,n异号,
由图可知:m<0,n>0.
又P(π,0),
∴T>π且
| 3T |
| 4 |
则π<T<
| 4π |
| 3 |
当周期无限接近π时,图中的最低点自左向右无限接近
| 3π |
| 4 |
∴f(x)在(
| 2π |
| 3 |
当周期接近
| 4π |
| 3 |
| 4π |
| 3 |
| π |
| 4 |
f(x)在(0,
| π |
| 4 |
图中的最低点的横坐标大于
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
∴正确的答案为B.
故选:B.
点评:本题考查y=Asin(ωx+φ)型的函数图象,考查了正弦函数的单调性,训练了利用排除法求解选择题,该题题目设置较为抽象,灵活性强.

练习册系列答案
相关题目
设全集I=R,M={x|x2>4},N={x|1<x<3},则(CIM)∩N为( )
| A、{x|x<2} |
| B、{x|1<x≤2} |
| C、{x|-2≤x<1} |
| D、{x|-2≤x≤2} |
下列函数,在其定义域内既是奇函数又是增函数的是( )
| A、y=2x(x∈R) | ||
| B、y=-log2x(x>0,x∈R) | ||
| C、y=x+x3(x∈R) | ||
D、y=-
|
已知条件p:a=2,条件q:圆C1:x2+y2=9与圆C2:(x-a)2+y2=1相切,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.
如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.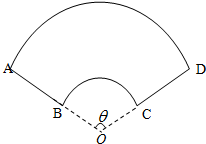 某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形.花坛设计周长为30米,其中大圆弧AD所在圆的半径为10米.设小圆弧BC所在圆的半径为x米(0<x<10),圆心角为θ弧度.