题目内容
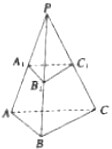 如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:
如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:| VP-ABC |
| VP-A1B1C1 |
| abc |
| a1b1c1 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:把棱锥P-A1B1C1看作棱锥C1-PA1B1,把棱锥P-ABC看作C-PAB,分别从C1和C作底面的高h1和h,由此利用等积法能证明
=
.
| VP-ABC |
| VP-A1B1C1 |
| abc |
| a1b1c1 |
解答:
证明:把棱锥P-A1B1C1看作棱锥C1-PA1B1,
把棱锥P-ABC看作C-PAB,
分别从C1和C作底面的高h1和h,
则
=
=
,
则VC1-PA1B1=
S△PA1B1•h1=
•
•a1b1sin∠A1PB1•h1,
VC-PAB=
S△PAB•h=
•
absin∠APB•h,
∴
=
=
=
.
把棱锥P-ABC看作C-PAB,
分别从C1和C作底面的高h1和h,
则
| h1 |
| h |
| PC1 |
| PC |
| c1 |
| c |
则VC1-PA1B1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
VC-PAB=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
∴
| VP-ABC |
| VP-A1B1C1 |
| VC1-PA1B1 |
| VC-PAB |
| ||||
|
| abc |
| a1b1c1 |
点评:本题考查等式的证明,是中档题,解题时要认真审题,注意等积法和空间思维能力的培养.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
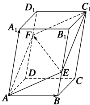 如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=
如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=