题目内容
将边长为2a的一块正方形铁皮的四角各截去一个大小相同的小正方形，然后将四边折起做成一个无盖的方盒．欲使所得的方盒有最大容积，截去的小正方形的边长应为多少？方盒的最大容积为多少？
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：设小正方形的边长为x，则盒底的边长为2a-2x，由于2a-2x＞0，则x∈（0，a），且方盒是以边长为2a-2x的正方形作底面，高为x的正方体，其体积为V=x（2a-2x）2，（x∈（0，a）），由此利用导数性质能求出结果．
解答：
解：设小正方形的边长为x，则盒底的边长为2a-2x，
由于2a-2x＞0，则x∈（0，a），
且方盒是以边长为2a-2x的正方形作底面，高为x的正方体，
其体积为V=x（2a-2x）2，（x∈（0，a））
V'=（2a-2x）（2a-6x），令V'=0，则x1=a，x2=
，
由x1=a∉（0，a），且对于x∈（0，
），V′＞0，x∈（
，a），V′＜0，
∴函数V在点x=
处取得极大值，由于问题的最大值存在，
∴V（
）=
即为容积的最大值，此时小正方形的边长为
．
由于2a-2x＞0，则x∈（0，a），
且方盒是以边长为2a-2x的正方形作底面，高为x的正方体，
其体积为V=x（2a-2x）2，（x∈（0，a））
V'=（2a-2x）（2a-6x），令V'=0，则x1=a，x2=
| a |
| 3 |
由x1=a∉（0，a），且对于x∈（0，
| a |
| 3 |
| a |
| 3 |
∴函数V在点x=
| a |
| 3 |
∴V（
| a |
| 3 |
| 16a3 |
| 27 |
| a |
| 3 |
点评：本题考查方盒了大容积的求法，是中档题，解题时要注意空间能力和导数性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
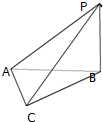如图，PB⊥平面ABC，△ABC为直角三角形，PB=BC=AC，∠ACB=90°．
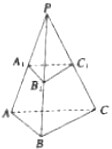如图所示，已知三棱锥P-ABC中，PA=a，PB=b，PC=c，侧棱PA、PB、PC上各有一点A1，B1、C1，且PA1=a1，PB1=b1，PC1=c1，求证：