题目内容
圆(x-1)2+y2=1和圆x2+y2-6y+5=0的位置关系为 .
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:分别求出两圆的圆心坐标和半径,利用圆心距与半径之和或半径之差的关系判断两圆的位置关系.
解答:
解:圆(x-1)2+y2=1的圆心C1(1,0),半径r1=1,
圆x2+y2-6y+5=0的圆心C2(0,3),半径r2=
=2,
|C1C2|=
=
>r1+r2=3,
∴两圆相离.
故答案为:相离.
圆x2+y2-6y+5=0的圆心C2(0,3),半径r2=
| 1 |
| 2 |
| 36-20 |
|C1C2|=
| 12+32 |
| 10 |
∴两圆相离.
故答案为:相离.
点评:本题考查两圆的位置关系的判断,是基础题,解题时要注意两点间距离公式的合理运用.

练习册系列答案
相关题目
对某班级50名学生学习数学与学习物理的成绩进行调查,得到如表所示:
由K2=
,解得K2=
≈11.5
参照附表,得到的正确结论是( )
| 数学成绩较好 | 数学成绩一般 | 合计 | |
| 物理成绩较好 | 18 | 7 | 25 |
| 物理成绩一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 50×(18×19-6×7)2 |
| 25×25×24×26 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A、在犯错误的概率不超过0.1%的前提下,认为“数学成绩与物理成绩有关” |
| B、在犯错误的概率不超过0.1%的前提下,认为“数学成绩与物理成绩无关” |
| C、有100%的把握认为“数学成绩与物理成绩有关” |
| D、有99%以上的把握认为“数学成绩与物理成绩无关” |
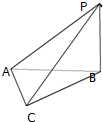 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.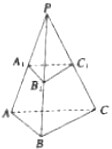 如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:
如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证: