题目内容
已知f（x）=x2+ax+3，当x∈[-1，1]时，f（x）＞a恒成立，求a的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：把f（x）=x2+ax+3代入f（x）＞a，分离参数a后得到a＜
，令 1-x=t换元，得到a＜t+
-2（0＜t≤2），求出函数g（t）=t+
-2（0＜t≤2）的最小值后得答案．
| x2+3 |
| 1-x |
| 4 |
| t |
| 4 |
| t |
解答：
解：由f（x）＞a，得x2+ax+3＞a，
即a（1-x）＜x2+3，
∵x∈[-1，1]，
当x=1时，对于任意实数a都成立；
当x≠1时，a＜
．
令 1-x=t，
则x=1-t，x2=t2-2t+1且-1≤1-t＜1，0＜t≤2，
则x2+3=t2-2t+4，
a＜
=t+
-2（0＜t≤2）．
令g（t）=t+
-2（0＜t≤2）．
则当t=2时函数g（t）有最小值为2．
∴a＜2．
综上，a＜2．
即a（1-x）＜x2+3，
∵x∈[-1，1]，
当x=1时，对于任意实数a都成立；
当x≠1时，a＜
| x2+3 |
| 1-x |
令 1-x=t，
则x=1-t，x2=t2-2t+1且-1≤1-t＜1，0＜t≤2，
则x2+3=t2-2t+4，
a＜
| t2-2t+4 |
| t |
| 4 |
| t |
令g（t）=t+
| 4 |
| t |
则当t=2时函数g（t）有最小值为2．
∴a＜2．
综上，a＜2．
点评：本题考查了函数恒成立问题，考查了数学转化思想方法，训练了分离参数法，考查了利用基本不等式求最值，是中档题．
练习册系列答案
相关题目
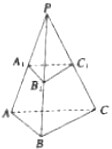如图所示，已知三棱锥P-ABC中，PA=a，PB=b，PC=c，侧棱PA、PB、PC上各有一点A1，B1、C1，且PA1=a1，PB1=b1，PC1=c1，求证：