题目内容
定义在R上的函数f（x）满足：f（x+y）=f（x）-f（y），那么此函数的奇偶性是 ．
考点：抽象函数及其应用
专题：函数的性质及应用
分析：先利用赋值法求出f（0）=0，再令y=-x，代入恒等式，则可得到f（-x）与f（x）的关系，然后判断奇偶性．
解答：
解：令x=y=0，代入f（x+y）=f（x）-f（y）得f（0）=0；
令y=-x，代入f（x+y）=f（x）-f（y）得
f（0）=f（x）-f（-x）=0，
所以f（-x）=f（x），
即原函数在定义域内是偶函数．
故答案为：偶函数．
令y=-x，代入f（x+y）=f（x）-f（y）得
f（0）=f（x）-f（-x）=0，
所以f（-x）=f（x），
即原函数在定义域内是偶函数．
故答案为：偶函数．
点评：本题考查了抽象函数的奇偶性，一般先采用赋值法求出f（0）的值，再设法用-x，x替换等式中的量，最终求出f（-x）与f（x）的关系．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
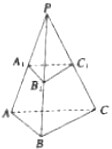如图所示，已知三棱锥P-ABC中，PA=a，PB=b，PC=c，侧棱PA、PB、PC上各有一点A1，B1、C1，且PA1=a1，PB1=b1，PC1=c1，求证：