题目内容
双曲线
-
=1的离心率e=
,则其渐近线方程为 .
| x2 |
| λ-2 |
| y2 |
| λ-4 |
| 2 | ||
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:讨论双曲线的焦点位置,分别求出a,b,c,再由离心率公式解出λ,再由双曲线方程写出渐近线方程.
解答:
解:当焦点在x轴上,λ-2>0且λ-4>0,
即有λ>4,a2=λ-2,b2=λ-4,c2=2λ-6.
即有e2=
=
,则λ=5.
则双曲线方程为
-y2=1,其渐近线方程为y=±
x;
当焦点在y轴上,λ-2<0且λ-4<0,
即有λ<2,a2=4-λ,b2=2-λ,c2=6-2λ.
即有e2=
=
,则λ=1.
则双曲线方程为
-x2=1,其渐近线方程为y=±
x.
故答案为:y=±
x或y=±
x
即有λ>4,a2=λ-2,b2=λ-4,c2=2λ-6.
即有e2=
| 2λ-6 |
| λ-2 |
| 4 |
| 3 |
则双曲线方程为
| x2 |
| 3 |
| ||
| 3 |
当焦点在y轴上,λ-2<0且λ-4<0,
即有λ<2,a2=4-λ,b2=2-λ,c2=6-2λ.
即有e2=
| 6-2λ |
| 4-λ |
| 4 |
| 3 |
则双曲线方程为
| y2 |
| 3 |
| 3 |
故答案为:y=±
| ||
| 3 |
| 3 |
点评:本题考查双曲线的方程和性质,主要是渐近线方程,考查分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知实数x,y满足
,记t=
的最大值为m,最小值为n,则m-n=( )
|
| y-1 |
| x+1 |
A、.
| ||
B、
| ||
C、-
| ||
D、-
|
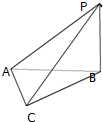 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.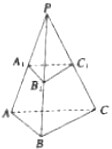 如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:
如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证: