题目内容
是否存在实数a,b,使y=
的最大值为9,最小值为1?
| ax2+8x+b |
| x2+1 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:化简y=
为(y-a)x2-8x+y-b=0,则△=64-4(y-a)(y-b)≥0,则1和9是y2-(a+b)y+ab-16=0的两个根,从而解出a,b.
| ax2+8x+b |
| x2+1 |
解答:
解:∵y=
,
∴y(x2+1)=ax2+8x+b,
∴(y-a)x2-8x+y-b=0,
那么△=64-4(y-a)(y-b)≥0,
即y2-(a+b)y+ab-16≤0,
依题意知1和9是y2-(a+b)y+ab-16=0的两个根,
那么a+b=1+9=10,ab-16=1×9=9,
即:a+b=10,ab=25,
即:a=b=5.
| ax2+8x+b |
| x2+1 |
∴y(x2+1)=ax2+8x+b,
∴(y-a)x2-8x+y-b=0,
那么△=64-4(y-a)(y-b)≥0,
即y2-(a+b)y+ab-16≤0,
依题意知1和9是y2-(a+b)y+ab-16=0的两个根,
那么a+b=1+9=10,ab-16=1×9=9,
即:a+b=10,ab=25,
即:a=b=5.
点评:本题考查了函数的最值的求法,化为二次函数,用韦达定理简化运算,属于中档题.

练习册系列答案
相关题目
已知f(x)=
;则f(2)=( )
|
| A、4 | B、2 | C、0 | D、1 |
已知实数x,y满足
,记t=
的最大值为m,最小值为n,则m-n=( )
|
| y-1 |
| x+1 |
A、.
| ||
B、
| ||
C、-
| ||
D、-
|
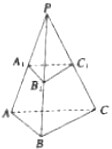 如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:
如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证: