题目内容
对于实数x,y,“x2+y2>2”是“|x|>1且|y|>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:画出“x2+y2>2”和“|x|>1且|y|>1”表示的平面区域,并分析两个区域的包含关系,进而利用集合法可得答案.
解答:
解:令A={(x,y)|x2+y2>2},B={(x,y)||x|>1且|y|>1}
则A表示的平面区域如下图中圆O外所示,B表示的平面区域如下图中正方形ABCD外所示:
:
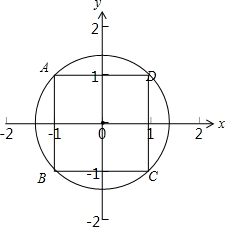
故B?A,
即“x2+y2>2”是“|x|>1且|y|>1”的必要不充分条件,
故选:B
则A表示的平面区域如下图中圆O外所示,B表示的平面区域如下图中正方形ABCD外所示:
:

故B?A,
即“x2+y2>2”是“|x|>1且|y|>1”的必要不充分条件,
故选:B
点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知函数f(x)=(sinx+cosx)2-1,x∈R,则f(x)的最小正周期是( )
| A、2π | ||
B、
| ||
| C、π | ||
D、
|
若变量x,y满足约束条件
,则z=4y-x的最大值为( )
|
| A、12 | B、16 | C、0 | D、32 |
函数f(x)=tanx-
在区间(0,
)内的零点个数是( )
| 1 |
| x |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
已知A={x|3-|x-2|≥0},B={y|y≥2},则A∩B=( )
| A、∅ | B、[2,5] |
| C、[-1,5] | D、[2,+∞) |
设a∈R,则“a=1”是“函数f(x)=(a-1)x3+(a2-1)x2+x为奇函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |