题目内容
设a∈R,则“a=1”是“函数f(x)=(a-1)x3+(a2-1)x2+x为奇函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据函数奇偶性的定义和性质,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:函数f(x)=(a-1)x3+(a2-1)x2+x为奇函数得a=±1,则必要性不成立,
当a=1时,f(x)=(a-1)x3+(a2-1)x2+x=x为奇函数,充分性成立,
故“a=1”是“函数f(x)=(a-1)x3+(a2-1)x2+x为奇函数”的充分不必要条件,
故选A.
当a=1时,f(x)=(a-1)x3+(a2-1)x2+x=x为奇函数,充分性成立,
故“a=1”是“函数f(x)=(a-1)x3+(a2-1)x2+x为奇函数”的充分不必要条件,
故选A.
点评:本题主要考查充分条件和必要条件的判断,利用函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
对于实数x,y,“x2+y2>2”是“|x|>1且|y|>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在区间(0,1)内任取两个数,则这两个数之和小于
的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若某空间几何体的三视图如图所示,则该几何体的体积是( )
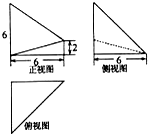

| A、16 | B、32 | C、48 | D、144 |
已知角α的终边过点P(
,-
),则sinα的值为( )
| 1 |
| 3 |
2
| ||
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知定义在R上的函数f(x)=ex+x2-x+sinx,则曲线y=f(x)在点(0,f(0))处的切线方程是( )
| A、y=2x-1 |
| B、y=x+1 |
| C、y=3x-2 |
| D、y=-2x+3 |
甲、乙两名考生在填报志愿时都选中了A、B、C、D四所需要面试的院校,这四所院校的面试安排在同一时间,因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位同学选择各个院校是等可能的,则甲、乙选择同一所院校的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知A={x|y=
},B={y|y=log2(x2+4)},则A∩B=( )
| 3-|x-2| |
| A、∅ | B、[2,5] |
| C、[-1,5] | D、[2,+∞] |