题目内容
若变量x,y满足约束条件
,则z=4y-x的最大值为( )
|
| A、12 | B、16 | C、0 | D、32 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答:
 解:由z=4y-x得y=
解:由z=4y-x得y=
x+
,
作出不等式组对应的平面区域如图(阴影部分):
平移直线y=
x+
,
由图象可知当直线y=
x+
,过点C时,直线y=
x+
的截距最大,此时z最大,
由
,解得
,即A(4,4).
代入目标函数z=4y-x,
得z=4×4-4=12.
故选:A.
 解:由z=4y-x得y=
解:由z=4y-x得y=| 1 |
| 4 |
| z |
| 4 |
作出不等式组对应的平面区域如图(阴影部分):
平移直线y=
| 1 |
| 4 |
| z |
| 4 |
由图象可知当直线y=
| 1 |
| 4 |
| z |
| 4 |
| 1 |
| 4 |
| z |
| 4 |
由
|
|
代入目标函数z=4y-x,
得z=4×4-4=12.
故选:A.
点评:本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
设随机变量X服从二项分布X~B(5,
),则函数f(x)=x2+4x+X存在零点的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于实数x,y,“x2+y2>2”是“|x|>1且|y|>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知复数z=i(1-i),z在复平面内对应的点Z(x,y)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知i是虚数单位,
的虚部是( )
| 1-3i |
| 2+i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
(1-2x)4(x+2)3的展开式中x2项的系数是( )
| A、294 | B、96 |
| C、102 | D、198 |
已知定义在R上的函数f(x)=ex+x2-x+sinx,则曲线y=f(x)在点(0,f(0))处的切线方程是( )
| A、y=2x-1 |
| B、y=x+1 |
| C、y=3x-2 |
| D、y=-2x+3 |
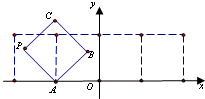 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断: