题目内容
已知A={x|3-|x-2|≥0},B={y|y≥2},则A∩B=( )
| A、∅ | B、[2,5] |
| C、[-1,5] | D、[2,+∞) |
考点:交集及其运算
专题:集合
分析:求解绝对值的不等式化简集合A,然后直接利用交集运算求解.
解答:
解:由3-|x-2|≥0,得|x-2|≤3,解得:-1≤x≤5.
∴A={x|3-|x-2|≥0}=[-1,5].
又B={y|y≥2}=[2,+∞),
∴A∩B=[2,5].

故选:B.
∴A={x|3-|x-2|≥0}=[-1,5].
又B={y|y≥2}=[2,+∞),
∴A∩B=[2,5].

故选:B.
点评:本题考查了交集及其运算,考查了绝对值不等式的解法,是基础题.

练习册系列答案
相关题目
对于实数x,y,“x2+y2>2”是“|x|>1且|y|>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i是虚数单位,
的虚部是( )
| 1-3i |
| 2+i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点为抛物线x2=4y的焦点,则直线l的方程为( )
| A、2x+3y-3=0 |
| B、x-y-1=0 |
| C、x+y-1=0 |
| D、x-y+1=0 |
(1-2x)4(x+2)3的展开式中x2项的系数是( )
| A、294 | B、96 |
| C、102 | D、198 |
在区间(0,1)内任取两个数,则这两个数之和小于
的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若某空间几何体的三视图如图所示,则该几何体的体积是( )
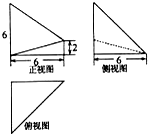

| A、16 | B、32 | C、48 | D、144 |
已知A={x|y=
},B={y|y=log2(x2+4)},则A∩B=( )
| 3-|x-2| |
| A、∅ | B、[2,5] |
| C、[-1,5] | D、[2,+∞] |