题目内容
20.已知函数f(x)=$\frac{1}{2}{x^2}$+alnx-bx,a,b为实数.(1)当b=0时,求函数f(x)的值域;
(2)当a=b=-1时,若a∈(1,e],求证:对任意s,t∈[1,a]恒有|f(s)-f(t)|<1.
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)问题转化为证明$\frac{1}{2}$a2-alna-$\frac{1}{2}$<1,记h(a)=$\frac{1}{2}$a2-alna-$\frac{3}{2}$,1<a≤e,根据合适的单调性证明即可.
解答 解:(1)b=0时,f′(x)=x+$\frac{a}{x}$,x>0,
a>0时,f′(x)>0,f(x)递增,f(x)的值域是R,
a=0时,f′(x)>0,f(x)递增,f(x)的值域是(0,+∞),
a<0时,由f′(x)=x+$\frac{a}{x}$=0,得x=$\sqrt{-a}$,
故f(x)在(0,$\sqrt{-a}$)递减,在($\sqrt{-a}$,+∞)递增,
故f(x)min=-$\frac{a}{2}$+aln($\sqrt{-a}$),f(x)的值域是[-$\frac{a}{2}$+aln$\sqrt{-a}$,+∞);
(2)证明:∵对于任意x∈[1,a],
f′(x)=$\frac{(x-a)(x-1)}{x}$≤0,
∴f(x)在[1,a]内单调递减,
于是|f(s)-f(t)|≤f(1)-f(a)=$\frac{1}{2}$a2-alna-$\frac{1}{2}$,
要证|f(s)-f(t)|<1,即证$\frac{1}{2}$a2-alna-$\frac{1}{2}$<1,
记h(a)=$\frac{1}{2}$a2-alna-$\frac{3}{2}$,1<a≤e,
则h′(a)=a-lna-1,h″(a)=1-$\frac{1}{a}$,
∵1<a≤e,∴1-$\frac{1}{a}$>0,∴h″(a)>0,
∴当1<a≤e时,h′(a)递增,
又h′(1)=0,∴h′(a)>0,
∴当1<a≤e时,h(a)递增,
∴h(a)max=h(e)=$\frac{(e-3)(e+1)}{2}$<0,
故命题成立.
点评 本题考查了函数的单调性、最值问题,考查导数的由应用以及分类讨论思想、考查不等式的证明,是一道中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
一次该商场要根据实际情况(如资金、劳动力(工资)等)准备好月资金工艺量,以使每月的总利润达到最大,通过一个月的市场调查,得到销售这两种产品的有关数据如表:
| 资金 | 产品所需资金(百元/台) | 月资金供应量(百元) | |
| 手机 | 空调 | ||
| 成本 | 40 | 30 | 600 |
| 劳动力(工资) | 2 | 5 | 58 |
| 利润 | 11 | 10 | |
| A. | x+3y=0 | B. | 3x-y=0 | C. | 3x-y-9=0 | D. | 3x+y+9=0 |
| A. | 100100 | B. | 10010 | C. | 10100 | D. | 1011001 |
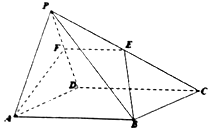 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.