题目内容
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为2,且两条渐近线与抛物线y2=2px(p>0)的准线交于A,B两点,O为坐标原点,若${S_{△AOB}}=\sqrt{3}$,则抛物线的方程为y2=4x.分析 求出抛物线的准线方程和双曲线的渐近线方程,运用代入法,求得AB,再由三角形的面积公式,结合离心率公式和a,b,c的关系,化简整理,解方程可得p,进而得到双曲线方程.
解答 解:抛物线y2=2px(p>0)的准线为x=-$\frac{p}{2}$,
双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的渐近线方程为y=±$\frac{b}{a}$x,
把x=-$\frac{p}{2}$代入y=±$\frac{b}{a}$x,
解得y=±$\frac{pb}{2a}$.
∴|AB|=$\frac{pb}{a}$,
∵△AOB的面积为$\sqrt{3}$,
∴$\frac{1}{2}$•$\frac{p}{2}$•$\frac{pb}{a}$=$\sqrt{3}$,
由e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=2,
解得$\frac{b}{a}$=$\sqrt{3}$.
∴$\frac{{p}^{2}}{4}$=1,
解得p=2.
∴该抛物线的标准方程是y2=4x.
故答案为:y2=4x.
点评 本题考查了双曲线与抛物线的标准方程及其性质,考查方程思想,考查推理能力与计算能力,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
6.已知集合A={x|log${\;}_{\frac{1}{2}}$x>-1},B=|x|2x>$\sqrt{2}$|,则A∪B=( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | (0,2) |
4.已知p:幂函数y=(m2-m-1)xm在(0,+∞)上单调递增;q:|m-2|<1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不要条件 |
1.已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F(-c,0)和虚轴端点E的直线交双曲线右支于点P,若E为线段EP的中点,则该双曲线的离心率为( )
| A. | $\sqrt{5}+1$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
8.正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则AD1与平面BB1D1所成角的正弦值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
5.某商场计划在今年同时出售智能手机和变频空调,两种市场销售情况很好(有多少就能卖多少)的新产品,
一次该商场要根据实际情况(如资金、劳动力(工资)等)准备好月资金工艺量,以使每月的总利润达到最大,通过一个月的市场调查,得到销售这两种产品的有关数据如表:
怎样确定这两种产品的月供应量,才能使每月的总利润最大,总利润的最大值是多少百元?
一次该商场要根据实际情况(如资金、劳动力(工资)等)准备好月资金工艺量,以使每月的总利润达到最大,通过一个月的市场调查,得到销售这两种产品的有关数据如表:
| 资金 | 产品所需资金(百元/台) | 月资金供应量(百元) | |
| 手机 | 空调 | ||
| 成本 | 40 | 30 | 600 |
| 劳动力(工资) | 2 | 5 | 58 |
| 利润 | 11 | 10 | |
6.已知角α是第四象限角,角α的终边经过点P(4,y),且sinα=$\frac{y}{5}$,则tanα的值是( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
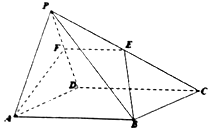 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.