题目内容
若函数f(x)=ex+lnx,g(x)=e-x+lnx,h(x)=e-x-lnx的零点依次为a,b,c,则a,b,c的大小为( )
| A、a>b>c |
| B、b>a>c |
| C、c>b>a |
| D、a>c>b |
考点:函数单调性的性质
专题:计算题,数形结合,函数的性质及应用
分析:分别由f(x)=0,g(x)=0,h(x)=0,得到两个函数关系,利用数形结合即可得到函数零点a,b,c的大小关系.
解答:
 解:∵f(x)=ex+lnx,g(x)=e-x+ln x,h(x)=e-x-ln x,
解:∵f(x)=ex+lnx,g(x)=e-x+ln x,h(x)=e-x-ln x,
∴由f(x)=0,g(x)=0,h(x)=0,
得ex+ln x=0,g(x)=e-x+ln x=0,h(x)=e-x-ln x=0,
即-ex=ln x,-e-x=ln x,e-x=ln x,
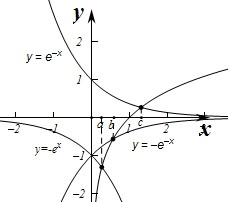
分别作出函数y=-ex,y=-e-x,y=-e-x,y=ln x的图象如图:
则由图象可知0<a<b<1<c,
即c>b>a,
故选:C.
 解:∵f(x)=ex+lnx,g(x)=e-x+ln x,h(x)=e-x-ln x,
解:∵f(x)=ex+lnx,g(x)=e-x+ln x,h(x)=e-x-ln x,∴由f(x)=0,g(x)=0,h(x)=0,
得ex+ln x=0,g(x)=e-x+ln x=0,h(x)=e-x-ln x=0,
即-ex=ln x,-e-x=ln x,e-x=ln x,
分别作出函数y=-ex,y=-e-x,y=-e-x,y=ln x的图象如图:
则由图象可知0<a<b<1<c,
即c>b>a,
故选:C.
点评:本题主要考查函数零点的大小判断,根据方程和函数之间的关系,将方程转化为两个函数的交点问题是解决本题的关键,注意利用数形结合的数学思想.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知x=log23-log2
,y=log0.5π,z=0.9-1.1,则( )
| 3 |
| A、x<y<z |
| B、z<y<x |
| C、y<z<x |
| D、y<x<z |
已知sinα=-
,并且α是第三象限角,那么tanα的值等于( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|