题目内容
14．若平面α∥β，直线a⊆α，直线b⊆β，那么直线a，b的位置关系是（ ）| A． | 相交 | B． | 平行 | C． | 异面 | D． | 平行或异面 |
分析 利用平面平行的性质及空间中直线与直线的位置关系求解．
解答 解：∵平面α∥β，直线a⊆α，直线b⊆β，
∴直线a，b一定没有交点，
∴直线a，b的位置关系是平行或异面．
故选：D．
点评 本题考查空间中两直线的位置关系的判断，是中档题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．下列选项中，说法正确的是（ ）
| A． | 若a＞b＞0，则${log_{\frac{1}{2}}}a＞{log_{\frac{1}{2}}}b$ | |
| B． | 向量$\overrightarrow a=（1，m），\overrightarrow b=（m，2m-1）$（m∈R）共线的充要条件是m=0 | |
| C． | 命题“?n∈N*，3n＞（n+2）•2n-1”的否定是“?n∈N*，3n≥（n+2）•2n-1” | |
| D． | 已知函数f（x）在区间[a，b]上的图象是连续不断的，则命题“若f（a）•f（b）＜0，则f（x）在区间（a，b）内至少有一个零点”的逆命题为假命题 |
5．不等式ax2+bx+c＜0的解集为空集，则（ ）
| A． | a＜0，△＞0 | B． | a＜0，△≥0 | C． | a＞0，△≤0 | D． | a＞0，△≥0 |
9．已知$cos（\frac{3π}{14}-θ）=\frac{1}{3}$，则$sin（\frac{2π}{7}+θ）$=（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $-\frac{{2\sqrt{2}}}{3}$ |
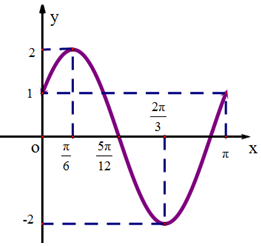已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示．
如图，已知平面ABC⊥平面BCDE，△DEF与△ABC分别是棱长为1与2的正三角形，AC∥DF，四边形BCDE为直角梯形，DE∥BC，BC⊥CD，CD=1，点G为△ABC的重心，N为AB中点，$\overrightarrow{AM}=λ\overrightarrow{AF}（λ∈R，λ＞0）$．