题目内容
6.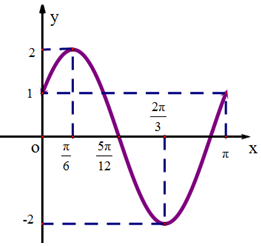 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.(1)求函数f(x)的解析式;
(2)求函数g(x)=lg[f(x)-1]的定义域.
分析 (1)由函数f(x)=Asin(ωx+φ)的部分图象得出A、ω与φ的值,即可写出f(x)的解析式;
(2)根据对数函数的定义,得出f(x)-1>0,再利用三角函数的图象与性质求出x的取值范围.
解答 解:(1)由函数f(x)=Asin(ωx+φ)的部分图象知,
A=2,
$\frac{T}{2}$=$\frac{2π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,
∴T=π,∴ω=$\frac{2π}{π}$=2;
又f($\frac{π}{6}$)=2sin(2×$\frac{π}{6}$+φ)=2,
∴φ=$\frac{π}{6}$+2kπ,k∈Z;
又|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{6}$;
∴f(x)=2sin(2x+$\frac{π}{6}$);
(2)∵函数g(x)=lg[f(x)-1],
∴f(x)-1>0,
∴f(x)>1;
又f(x)=2sin(2x+$\frac{π}{6}$),
∴sin(2x+$\frac{π}{6}$)>$\frac{1}{2}$,
∴$2kπ+\frac{π}{6}<2x+\frac{π}{6}<2kπ+\frac{5π}{6}$,
解得kπ<x<kπ+$\frac{π}{3}$,k∈Z;
∴g(x)的定义域为$\left\{{x|kπ<x<kπ+\frac{π}{3},k∈Z}\right\}$.
点评 本题考查了由y=Asin(ωx+φ)的部分图象确定解析式,以及对数函数的定义域问题,是基础题目.

练习册系列答案
相关题目
14.若平面α∥β,直线a⊆α,直线b⊆β,那么直线a,b的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 异面 | D. | 平行或异面 |
11.给出下面四个命题(其中m,n,l为空间中不同的直线,α,β是空间中不同的平面)中正确的命题为( )
| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
15.已知$sin2θ-4sin({θ+\frac{π}{3}})sin({θ-\frac{π}{6}})=\frac{{\sqrt{3}}}{3}$,则cos2θ等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{\sqrt{3}}}{6}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |