题目内容
19.如果三点A(2,1),B(-2,a),C(6,8)在同一直线上,在a=-6.分析 由于A(2,1),B(-2,a),C(6,8)三点在同一直线上,可得kAB=kAC.解出即可.
解答 解:∵A(2,1),B(-2,a),C(6,8)三点在同一直线上,
∴kAB=kAC.
∴$\frac{a-1}{-2-2}=\frac{8-1}{6-2}$,
解得a=-6.
故答案为:-6.
点评 本题考查了三点共线与斜率的关系,属于基础题.

练习册系列答案
相关题目
9.设函数f(x)=alnx-bx2(x>0),若函数y=f(x)在x=1处与直线y=-1相切.
(Ⅰ) 求实数a,b的值;
(Ⅱ) 求函数y=f(x)在$[{\frac{1}{e},e}]$上的最大值.
(Ⅰ) 求实数a,b的值;
(Ⅱ) 求函数y=f(x)在$[{\frac{1}{e},e}]$上的最大值.
14.若平面α∥β,直线a⊆α,直线b⊆β,那么直线a,b的位置关系是( )
| A. | 相交 | B. | 平行 | C. | 异面 | D. | 平行或异面 |
11.给出下面四个命题(其中m,n,l为空间中不同的直线,α,β是空间中不同的平面)中正确的命题为( )
| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
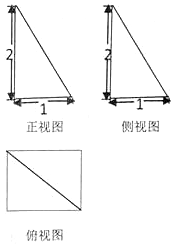 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点. 已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.
已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.