题目内容
4. 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.(1)当$λ=\frac{2}{3}$时,求证:GM∥平面DFN;
(2)若$λ=\frac{1}{2}$时,试求二面角M-BC-D的余弦值.
分析 (1)当λ=$\frac{2}{3}$时,连AG延长交BC于P,证明GM∥PF,P,D,F,N四点共面,即可证明:GM∥平面DFN.
(2)当$λ=\frac{1}{2}$时,以P为原点,PC为x轴,PE为y轴,PA为z轴建立空间直角坐标系,利用向量的夹角公式求二面角M-BC-D的余弦值
解答 证明:(1)连AG延长交BC于P,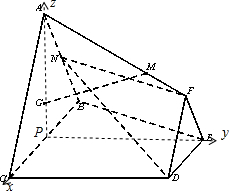
因为点G为△ABC的重心,所以$\frac{AG}{AP}$=$\frac{2}{3}$,(1分)
又$\overrightarrow{AM}$=λ$\overrightarrow{AF}$,λ=$\frac{2}{3}$,所以$\frac{AG}{AP}$=$\frac{AM}{AF}$=$\frac{2}{3}$,
所以GM∥PF,(2分)
因为AC∥DF,DE∥BC,所以平面ABC∥平面DEF,
又△DEF与△ABC分别是棱长为1与2的正三角形,
N为AB中点,P为BC中点,所以NP∥AC,
又AC∥DF,(3分)
所以NP∥DF,得P,D,F,N四点共面,
∴GM∥平面DFN.(5分)
解:(2)∵平面ABC⊥平面BCDE,∴平面DEF⊥平面BCDE,
以P为原点,PC为x轴,PE为y轴,PA为z轴建立空间直角坐标系,
则C(1,0,0),D(1,1,0),A(0,0,$\sqrt{3}$),F($\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$),B(-1,0,0),N(-$\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),(7分)
设M(x,y,z),
∵$\overrightarrow{AM}$=λ$\overrightarrow{AF}$,∴M($\frac{λ}{2}$,λ,$\sqrt{3}$-$\frac{\sqrt{3}}{2}λ$),$\overrightarrow{NM}$=($\frac{λ+1}{2}$,λ,$\frac{\sqrt{3}}{2}$(1-λ)),$\overrightarrow{CD}$=(0,1,0),
∵λ=$\frac{1}{2}$,∴M($\frac{1}{4}$,$\frac{1}{2}$,$\frac{3\sqrt{3}}{4}$),(9分)
设平面MBC的法向量$\overrightarrow{n}$=(a,b,c),$\overrightarrow{BC}$=(2,0,0),$\overrightarrow{BM}$=($\frac{5}{4}$,$\frac{1}{2}$,$\frac{3\sqrt{3}}{4}$),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=2a=0}\\{\overrightarrow{n}•\overrightarrow{BM}=\frac{5}{4}a+\frac{1}{2}b+\frac{3\sqrt{3}}{4}c=0}\end{array}\right.$,取c=-2,得$\overrightarrow{n}$=(0,3$\sqrt{3}$,-2),
面BCD的法向量$\overrightarrow{m}$=(0,0,1),
设二面角M-BC-D的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{31}}$=$\frac{2\sqrt{31}}{31}$,
∴二面角M-BC-D的余弦值为$\frac{2\sqrt{31}}{31}$.(12分)
点评 本题考查线面平行的证明,考查二面角M-BC-D的余弦值,考查向量方法的运用,属于中档题.

| A. | 相交 | B. | 平行 | C. | 异面 | D. | 平行或异面 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{\sqrt{3}}}{6}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
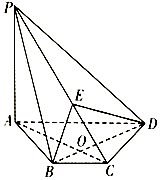 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.