题目内容
已知函数f(x)=
sin2xsinφ+cos2xcosφ-sin(
+φ)(0<φ<
),且函数图象过点(
,
).
(Ⅰ)求φ的值;
(Ⅱ)将函数 y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数y=g(x)的图象求函数y=g(x)在区间[0,
]上的最大值和最小值.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 4 |
(Ⅰ)求φ的值;
(Ⅱ)将函数 y=f(x)的图象上各点的横坐标缩短到原来的
| 2 |
| 3 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)利用两角和公式和二倍角公式对函数解析式化简,把点(
,
)代入求得φ.
(Ⅱ)根据题意得出g(x)的函数解析式,利用x的范围和三角函数的性质求得函数g(x)的最大和最小值.
| π |
| 4 |
| 1 |
| 4 |
(Ⅱ)根据题意得出g(x)的函数解析式,利用x的范围和三角函数的性质求得函数g(x)的最大和最小值.
解答:
解:(Ⅰ)f(x)=
sin2xsinφ+cos2xcosφ-sin(
+φ)
=
sin2xsinφ+
(1+cos2x)cosφ-
cosφ
=
sin2xsinφ+
cos2xcosφ
=
cos(2x-φ)
∵函数图象过点(
,
).
∴
=
cos(
-φ),即cos(
-φ)=sinφ=
,
∵0<φ<
,
∴φ=
(Ⅱ)由题意可知y=g(x)=f(
x)=
cos(3x-
),
∵x∈[0,
]
∴(3x-
)∈[-
,
],
∴-
≤cos(3x-
)≤1
∴函数y=g(x)在区间[0,
]上的最大值为
,最小值为-
.
| 1 |
| 2 |
| π |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∵函数图象过点(
| π |
| 4 |
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
∵0<φ<
| π |
| 2 |
∴φ=
| π |
| 6 |
(Ⅱ)由题意可知y=g(x)=f(
| 3 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵x∈[0,
| π |
| 3 |
∴(3x-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| ||
| 2 |
| π |
| 6 |
∴函数y=g(x)在区间[0,
| π |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
点评:本题主要考查了三角函数恒等变换的应用和三角函数图象与性质.解题关键就是要化繁为间,化难为易.

练习册系列答案
相关题目
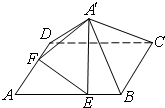 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2