题目内容

已知a＜b＜|a|，则以下不等式中恒成立的是（　　）
A、|b|＜-a
B、ab＞0
C、ab＜0
D、|a|＜|b|
考点：不等式比较大小
专题：不等式的解法及应用
分析：由a＜b＜|a|，可得a＜0，即可得出．
解答： 解：∵a＜b＜|a|，
∴a＜0，
∴|b|＜|a|=-a，
故选：A．
点评：本题考查了不等式的基本性质，考查了推理能力，属于基础题．
练习册系列答案
相关题目
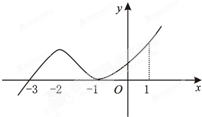如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：
①-3数y=f（x）的极值点；
②-1函数y=f（x）的最小值；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-3，1）上单调递增．
则正确命题的序号是（　　）
A、①②B、①④C、②③D、③④
以下四种化简过程，其中正确的有（　　）个．
①sin（360°+200°）=sin200°
②sin（180°-200°）=-sin200°
③sin（180°+200°）=sin200°
④sin（-200°）=sin200°．
A、1B、2C、3D、4
函数y=3sin（
π
3
-x）-cos（
π
6
+x），（x∈R）的最小值等于（　　）
A、-3
B、-2
C、-1
D、-
10
下列说法正确的是（　　）
A、单位向量都相等
B、长度相等的两个向量一定是共线向量
C、零向量没有方向
D、对于任意向量
a
，
b
，必有|
a
+
b
|≤|
a
|+|
b
|
sin（
π
6
+α）=
1
3
，则cos（
π
3
-α）的值为（　　）
A、
1
2
B、-
1
2
C、
1
3
D、-
1
3
已知F1、F2是椭圆
x2
36
+
y2
25
=1的两个焦点，A、B是椭圆上的两个点且其连线过F1，则△ABF2的周长为（　　）
A、12B、24C、36D、48
函数f（x）=1+
4-x2
（-2≤x≤2）与函数g（x）=m（x-2）+4．若函数h（x）=f（x）-g（x）有两个零点时，参数m的取值范围为（　　）
A、[
1
2
，
2
3
]
B、（-
1
2
，
2
3
）
C、[
5
12
，
3
4
]
D、（
5
12
，
3
4
]
已知|
a
|=2，|
b
|=4．
（1）当
a
∥
b
且方向相同时，求
a
•
b
；
（2）当
a
⊥
b
时，求|
a
+
b
|；
（3）若
a
+2
b
与3
a
-
b
垂直，求向量
a
和
b
的夹角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网