题目内容
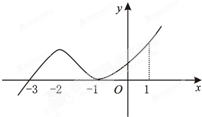 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3数y=f(x)的极值点;
②-1函数y=f(x)的最小值;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
考点:利用导数研究函数的单调性
专题:数形结合,导数的概念及应用
分析:根据导数的几何意义,与函数的单调性,极值点关系,结合图象判断.
解答:
解:根据f′(x)>0,f′(x)<0,可以确定函数的增区间,减区间,切线斜率的正负.
由导函数y=f′(x)的图象,可判断,f′(x)=0,x=-3.x=-1,
-3的左边负右边正,两边互为异号,
所以可判断f(x)单调性在(-∞,-3)为上减函数,(-3,-1)为增函数,
由上述条件可判断:
①-3是y=f(x)的极值点;④y=f(x)在区间(-3,1)上单调递增.两个结论正确.
②-1函数y=f(x)的最小值;③y=f(x)在x=0处切线的斜率小于零;两个结论错误.
故选:B
由导函数y=f′(x)的图象,可判断,f′(x)=0,x=-3.x=-1,
-3的左边负右边正,两边互为异号,
所以可判断f(x)单调性在(-∞,-3)为上减函数,(-3,-1)为增函数,
由上述条件可判断:
①-3是y=f(x)的极值点;④y=f(x)在区间(-3,1)上单调递增.两个结论正确.
②-1函数y=f(x)的最小值;③y=f(x)在x=0处切线的斜率小于零;两个结论错误.
故选:B
点评:本题考查了导数的图象在判断极值,单调区间中的运用,导数的几何意义的理解.

练习册系列答案
相关题目
从抛物线y2=8x上各点向x轴作垂线段,则垂线段中点的轨迹方程为( )
| A、y2=4x | ||
| B、y2=2x | ||
| C、y2=x | ||
D、y2=
|
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定分类变量“X和Y有关系”的可信度.如果K2的观测值为7.8,则下列说法中正确的是( )
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A、在犯错误的概率不超过1%的前提下,认为“X和Y有关系” |
| B、在犯错误的概率不超过1%的前提下,认为“X和Y有关系” |
| C、有99.5%以上的把握认为“X和Y有关系” |
| D、有99.5%以上的把握认为“X和Y有关系” |
在(
+
)100的展开式中,有理项的个数是( )
| 2 |
| 3 | 5 |
| A、15个 | B、33个 |
| C、17个 | D、16个 |
已知cos(π-α)=
,则cos2α的值是( )
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
(文科)不等式|x|-1≤0的解集为( )
| A、(-∞,1] |
| B、[-1,1] |
| C、(-∞,0] |
| D、[0,1] |
对于函数y=cos
,下列判断正确的是( )
| x |
| 2 |
| A、周期为2π的奇函数 | ||
B、周期为
| ||
| C、周期为π的偶函数 | ||
| D、周期为4π的偶函数 |
已知向量
=(2cosα,2sinα),
=(2sinβ,2cosβ),|
+
|=
,则sin(α+β)的值为( )
| m |
| n |
| m |
| n |
8
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a<b<|a|,则以下不等式中恒成立的是( )
| A、|b|<-a |
| B、ab>0 |
| C、ab<0 |
| D、|a|<|b| |