题目内容
函数f（x）=2x-3的零点所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
考点：二分法求方程的近似解
专题：计算题,函数的性质及应用
分析：易知函数f（x）=2x-3在R上连续且单调递增，从而由函数的零点的判定定理判断即可．
解答：
解：易知函数f（x）=2x-3在R上连续且单调递增，
f（1）=2-3=-1＜0，f（2）=4-3=1＞0；
故f（1）•f（2）＜0，
故函数f（x）=2x-3的零点所在的区间为（1，2）；
故选：B．
f（1）=2-3=-1＜0，f（2）=4-3=1＞0；
故f（1）•f（2）＜0，
故函数f（x）=2x-3的零点所在的区间为（1，2）；
故选：B．
点评：本题考查了函数的零点的判定定理的应用，属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
如图，在△ABC中，∠ABC=90°，以AB为直径的圆O交AC于点E，点D是BC边上的中点，连接OD交圆O与点M．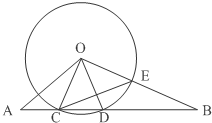
如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点．如图，正六边形ABCDEF中，AB=2，则（
-
）•（
+
）=（ ）
| BC |
| BA |
| AF |
| BC |
| A、-6 | ||
B、-2
| ||
C、2
| ||
| D、6 |