题目内容
已知函数f(x)=|sinx-a|,a∈R.
(1)试讨论函数f(x)的奇偶性;
(2)求当f(x)取得最大值时,自变量x的取值范围.
(1)试讨论函数f(x)的奇偶性;
(2)求当f(x)取得最大值时,自变量x的取值范围.
考点:函数的最值及其几何意义,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(1)对a的值进行讨论,结合奇偶函数的定义,即可得出结论;
(2)对a的值进行讨论,结合正弦函数的最值,即可得出结论.
(2)对a的值进行讨论,结合正弦函数的最值,即可得出结论.
解答:
解:(1)若a=0,则f(x)=|sinx|,此时f(-x)=|sin(-x)|=|-sinx|=|sinx|=f(x),所以函数为偶函数;若a不等于零,则函数不具有奇偶性;
(2)若a≥0,则函数的最大值为|1+a|,此时x=k•360°-90°;
若a<0,则函数的最大值为|1+a|,此时x=k•360°+90°.
(2)若a≥0,则函数的最大值为|1+a|,此时x=k•360°-90°;
若a<0,则函数的最大值为|1+a|,此时x=k•360°+90°.
点评:本题考查奇偶函数的定义,正弦函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=2x-3的零点所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
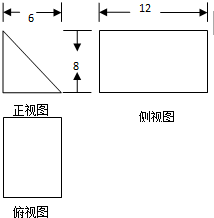 已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )
已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )A、
| ||
B、
| ||
| C、36π | ||
D、
|