题目内容
已知点R(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M(x,y)在直线PQ上,且2
+3
=0,
•
=0,则4x+2y-3的最小值为 .
| PM |
| MQ |
| RP |
| PM |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,设Q(a,0),P(0,b),由2
+3
=0,可得2(x,y-b)+3(a-x,-y)=0,可得b=-
y.由
•
=0,可得(3,b)•(x,y-b)=0,可得4x=y2,因此4x+2y-3=y2+2y-3=(y+1)2-4,利用二次函数的单调性即可得出.
| PM |
| MQ |
| 1 |
| 2 |
| RP |
| PM |
解答:
解:如图所示,
设Q(a,0),P(0,b),
∵2
+3
=0,
∴2(x,y-b)+3(a-x,-y)=0,
∴2x+3(a-x)=0,2(y-b)-3y=0,
解得a=
x,b=-
y.
∵
•
=0,
∴(3,b)•(x,y-b)=0,
∴3x+b(y-b)=0,
∵3x-
y(y+
y)=0,
化为4x=y2,
∴4x+2y-3=y2+2y-3=(y+1)2-4≥-4.
∴4x+2y-3的最小值为-4.
故答案为:-4.

设Q(a,0),P(0,b),
∵2
| PM |
| MQ |
∴2(x,y-b)+3(a-x,-y)=0,
∴2x+3(a-x)=0,2(y-b)-3y=0,
解得a=
| 1 |
| 3 |
| 1 |
| 2 |
∵
| RP |
| PM |
∴(3,b)•(x,y-b)=0,
∴3x+b(y-b)=0,
∵3x-
| 1 |
| 2 |
| 1 |
| 2 |
化为4x=y2,
∴4x+2y-3=y2+2y-3=(y+1)2-4≥-4.
∴4x+2y-3的最小值为-4.
故答案为:-4.
点评:本题考查了向量的坐标运算、数量积运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
设复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1-2i,则
的虚部为( )
| z2 |
| z1 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知集合M={x|
≥0},则∁RM=( )
| 1+x |
| 1-x |
| A、{x|-1<x<1} |
| B、{x|-1<x≤1} |
| C、{x|x<-1或x≥1} |
| D、{x|x≤-1或x≥1} |
函数f(x)=2x-3的零点所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
函数f(x)=log2(x+1)+2的零点所在区间是( )
A、(-
| ||||
B、(
| ||||
C、(-1,
| ||||
D、(1,
|
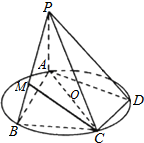 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=