题目内容
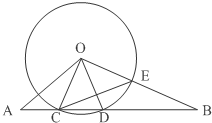如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点．（1）求BD长；
（2）当CE⊥OD时，求证：AO=AD．
考点：相似三角形的判定
专题：推理和证明
分析：（1）证明△OBD∽△AOC，通过比例关系求出BD即可．
（2）通过三角形的两角和，求解角即可．
（2）通过三角形的两角和，求解角即可．
解答：
解：（1）∵OC=OD，∴∠OCD=∠ODC，∴∠OAC=∠ODB．
∵∠BOD=∠A，∴△OBD∽△AOC．∴
=
，
∵OC=OD=6，AC=4，∴
=
，∴BD=9．…（5分）
（2）证明：∵OC=OE，CE⊥OD．∴∠COD=∠BOD=∠A．
∴∠AOD=180°-∠A-∠ODC=180°-∠COD-∠OCD=∠ADO．
∴AD=AO …（10分）
∵∠BOD=∠A，∴△OBD∽△AOC．∴
| BD |
| OC |
| OD |
| AC |
∵OC=OD=6，AC=4，∴
| BD |
| 6 |
| 6 |
| 4 |
（2）证明：∵OC=OE，CE⊥OD．∴∠COD=∠BOD=∠A．
∴∠AOD=180°-∠A-∠ODC=180°-∠COD-∠OCD=∠ADO．
∴AD=AO …（10分）
点评：本题考查三角形相似，角的求法，考查推理与证明，距离的求法．
练习册系列答案
相关题目
在区间[-3，2]上随机选取一个数x，使得函数y=
有意义的概率为（ ）
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
复数
（i为虚数单位）的虚部为（ ）
| 2+i |
| 2-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M={x|
≥0}，则∁RM=（ ）
| 1+x |
| 1-x |
| A、{x|-1＜x＜1} |
| B、{x|-1＜x≤1} |
| C、{x|x＜-1或x≥1} |
| D、{x|x≤-1或x≥1} |
函数f（x）=2x-3的零点所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |