题目内容
已知函数f(x)=cosx(sinx-
cosx)+
(Ⅰ)求函数f(x)的最小正周期及单调递减区间
(Ⅱ)求函数f(x)在区间[0,
]上的最大值和最小值.
| 3 |
| ||
| 2 |
(Ⅰ)求函数f(x)的最小正周期及单调递减区间
(Ⅱ)求函数f(x)在区间[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)首先利用三角函数关系式的恒等变换,把函数的关系式变形成正弦型函数,进一步求出函数的最小正周期和函数的单调区间.
(Ⅱ)利用函数的定义域直接求出函数的值域.
(Ⅱ)利用函数的定义域直接求出函数的值域.
解答:
解:(Ⅰ)f(x)=cosx(sinx-
cosx)+
=cosxsinx-
cos2x)+
=
sin2x-
cos2x
=sin(2x-
)
所以函数f(x)的最小正周期为:T=
=π
令:
+2kπ≤2x-
≤
+2kπ(k∈Z)
解得:
+kπ≤x≤
+kπ
所以函数的单调递减区间为:[
+kπ,
+kπ](k∈Z)
(Ⅱ)由于:0≤x≤
所以:-
≤2x-
≤
则:-
≤sin(2x-
)≤1
函数f(x)的最大值为1,函数的最小值为-
.
| 3 |
| ||
| 2 |
=cosxsinx-
| 3 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 3 |
所以函数f(x)的最小正周期为:T=
| 2π |
| 2 |
令:
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得:
| 5π |
| 12 |
| 11π |
| 12 |
所以函数的单调递减区间为:[
| 5π |
| 12 |
| 11π |
| 12 |
(Ⅱ)由于:0≤x≤
| π |
| 2 |
所以:-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
则:-
| ||
| 2 |
| π |
| 3 |
函数f(x)的最大值为1,函数的最小值为-
| ||
| 2 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的周期和单调性的应用,利用函数的定义域求函数的值域.属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数
(i为虚数单位)的虚部为( )
| 2+i |
| 2-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2x-3的零点所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
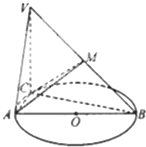 如图,已知⊙O的直径AB=3,点C为⊙O上异于A、B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(Ⅰ)求证:BC⊥平面VAC
如图,已知⊙O的直径AB=3,点C为⊙O上异于A、B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(Ⅰ)求证:BC⊥平面VAC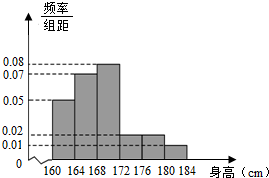 贵州省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
贵州省2014年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.