题目内容
函数f(x)=loga(4-ax)在区间[0,6]上为增函数,则a的取值范围是 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:根据题意利用复合函数的单调性可得0<a<1,再根据x=6时,t=4-6a>0,求得a的范围,再把这两个a的范围取交集,即得所求.
解答:
解:由题意可得a>0,a≠1,函数f(x)=loga(4-ax)在区间[0,6]上为增函数,而函数t=4-ax在区间[0,6]上为减函数,
∴0<a<1.
再根据x=6时,t=4-6a>0,求得a<
.
综上可得,a的范围是(0,
),
故答案为:(0,
).
∴0<a<1.
再根据x=6时,t=4-6a>0,求得a<
| 2 |
| 3 |
综上可得,a的范围是(0,
| 2 |
| 3 |
故答案为:(0,
| 2 |
| 3 |
点评:本题主要考查复合函数的单调性,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
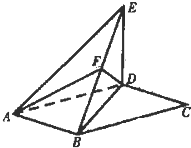 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD. 教室中用两根细绳悬吊的日光灯管如图所示,若将它绕中轴线扭转60°,灯管将上升
教室中用两根细绳悬吊的日光灯管如图所示,若将它绕中轴线扭转60°,灯管将上升