题目内容
已知圆C过点A(0,-2),B(3,1),且圆心C在直线x+2y+1=0上.
(Ⅰ)求圆C的标准方程;
(Ⅱ)直线l过点P(2,0),且与圆C交于M,N两点,若|MN|=4
,求直线l的方程.
(Ⅰ)求圆C的标准方程;
(Ⅱ)直线l过点P(2,0),且与圆C交于M,N两点,若|MN|=4
| 2 |
考点:直线与圆相交的性质,圆的标准方程
专题:直线与圆
分析:(1)设圆心C(-2b-1,b),再根据圆C过点A(0,-2),B(3,1),可得 (-2b-1-0)2+(b+2)2=(-2b-1-3)2+(b-1)2=r2,r为半径.解得b的值,可得圆心C和半径r,从而求得圆C的标准方程.
(Ⅱ)由题意根据弦长公式求得弦心距d=1.分直线的斜率不存在、存在两种情况,分别根据弦心距d=
=1,求得直线的方程.
(Ⅱ)由题意根据弦长公式求得弦心距d=1.分直线的斜率不存在、存在两种情况,分别根据弦心距d=
| |k+2| | ||
|
解答:
解:(1)∵圆心C在直线x+2y+1=0上,故设圆心C(-2b-1,b),再根据圆C过点A(0,-2),B(3,1),
可得 (-2b-1-0)2+(b+2)2=(-2b-1-3)2+(b-1)2=r2,r为半径.
解得b=-2,可得圆心C(3,-2),r=3,
∴圆C的标准方程为 (x-3)2+(y+2)2=9.
(Ⅱ)直线l过点P(2,0),且与圆C交于M,N两点,若|MN|=4
,则弦心距d=1.
当直线的斜率不存在时,直线的方程为x=2,满足弦心距d=1.
当直线的斜率存在时,设直线的方程为y-0=k(x-2),根据弦心距d=
=1,求得k=-
.
此时,直线的方程为3x+4y-6=0.
综上可得,所求的直线的方程为 x=2,或3x+4y-6=0.
可得 (-2b-1-0)2+(b+2)2=(-2b-1-3)2+(b-1)2=r2,r为半径.
解得b=-2,可得圆心C(3,-2),r=3,
∴圆C的标准方程为 (x-3)2+(y+2)2=9.
(Ⅱ)直线l过点P(2,0),且与圆C交于M,N两点,若|MN|=4
| 2 |
当直线的斜率不存在时,直线的方程为x=2,满足弦心距d=1.
当直线的斜率存在时,设直线的方程为y-0=k(x-2),根据弦心距d=
| |k+2| | ||
|
| 3 |
| 4 |
此时,直线的方程为3x+4y-6=0.
综上可得,所求的直线的方程为 x=2,或3x+4y-6=0.
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
相关题目
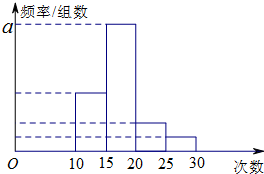 对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下:
对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下: