题目内容
方程
+
=10，化简的结果是 ．
| (x-2)2+y2 |
| (x+2)2+y2 |
考点：椭圆的定义
专题：圆锥曲线的定义、性质与方程
分析：根据方程得出它表示的几何意义是椭圆，从而求出方程化简的结果是椭圆的标准方程．
解答：
解：∵方程
+
=10，
表示平面内到定点F1（-2，0）、F2（2，0）的距离的和是常数10（10＞4）的点的轨迹，
∴它的轨迹是以F1、F2为焦点，长轴2a=10，焦距2c=4的椭圆；
∴a=5，c=2，b=
=
；
∴椭圆的方程是
+
=1，即为化简的结果．
故答案为：
+
=1．
| (x-2)2+y2 |
| (x+2)2+y2 |
表示平面内到定点F1（-2，0）、F2（2，0）的距离的和是常数10（10＞4）的点的轨迹，
∴它的轨迹是以F1、F2为焦点，长轴2a=10，焦距2c=4的椭圆；
∴a=5，c=2，b=
| 52-22 |
| 21 |
∴椭圆的方程是
| x2 |
| 25 |
| y2 |
| 21 |
故答案为：
| x2 |
| 25 |
| y2 |
| 21 |
点评：本题考查了椭圆的定义问题，解题时应根据题意得出方程表示的几何意义是什么，从而得到化简的结果，是基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
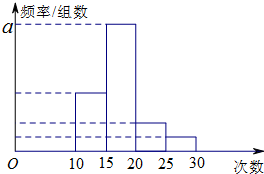对某校高三学生一个月内参加体育活动的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加体育活动的次数．根据此数据做出了频数与频率的统计表和频率分布直方图如下：