题目内容
已知tanα=-2，求4sin2α+3cos2α的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式分母看做“1”，利用同角三角函数间基本关系化简，再弦化切后将tanα的值代入计算即可求出值．
解答：
解：∵tanα=-2，
∴原式=
=
=
=
．
∴原式=
| 4sin2α+3cos2α |
| sin2α+cos2α |
| 4tan2α+3 |
| tan2α+1 |
| 16+3 |
| 4+1 |
| 19 |
| 5 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
已知α，β是任意角，则“sinα=cosα”是“cos（α+β）=sin（α-β）”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
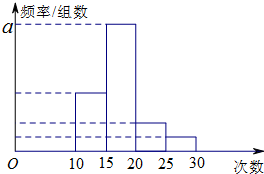对某校高三学生一个月内参加体育活动的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加体育活动的次数．根据此数据做出了频数与频率的统计表和频率分布直方图如下：