题目内容
13.已知△ABC的三内角A,B,C,所对三边分别为a,b,c,sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,若△ABC的面积S=24,b=10,则a的值是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 利用差角的正弦公式,即可求sinA,cosA的值,利用三角形面积公式可求c,利用余弦定理求a的值.
解答 解:∵sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,
∴$\frac{\sqrt{2}}{2}$(sinA-cosA)=$\frac{\sqrt{2}}{10}$,
∴sinA-cosA=$\frac{1}{5}$,
∴sinAcosA=$\frac{12}{25}$,
∴sinA=$\frac{4}{5}$,cosA=$\frac{3}{5}$,
∵△ABC的面积S=24,b=10,
∴24=$\frac{1}{2}$bcsinA=$\frac{1}{2}×10×c×\frac{4}{5}$,
∴c=6,
∴a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=8.
故选:D.
点评 本题考查差角的正弦公式、三角形的面积公式,考查余弦定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
5.方程xy(x+y)=1所表示的曲线( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
3.设函数$f(x)=\left\{\begin{array}{l}{log_2}(-x),x<0\\{2^x},x≥0\end{array}\right.$,若关于x的方程f2(x)-af(x)=0恰有三个不同的实数根,则实数a的取值范围是( )
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
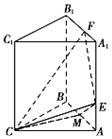 在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点
在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AAl,A1B1上,且AE=$\frac{1}{2}$,A1F=$\frac{3}{4}$,CE⊥EF,M为AB中点