题目内容
2.已知{an}是正项等差数列,数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和Sn=$\frac{n}{2n+4}$,若bn=(-1)n•an2,则数列{bn}的前n项和T2n=2n2+3n.分析 设正项等差数列{an}的公差为d>0,由数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和Sn=$\frac{n}{2n+4}$,可得$\frac{1}{{a}_{1}({a}_{1}+d)}$=$\frac{1}{6}$,$\frac{1}{6}$+$\frac{1}{({a}_{1}+d)({a}_{1}+2d)}$=$\frac{2}{8}$,解得a1,d.可得an.可得b2n-1+b2n,即可得出.
解答 解:设正项等差数列{an}的公差为d>0,∵数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和Sn=$\frac{n}{2n+4}$,
∴$\frac{1}{{a}_{1}({a}_{1}+d)}$=$\frac{1}{6}$,$\frac{1}{6}$+$\frac{1}{({a}_{1}+d)({a}_{1}+2d)}$=$\frac{2}{8}$,解得a1=2,d=1.
∴an=2+(n-1)=n+1.
∴bn=(-1)n•an2=(-1)n(n+1)2,
b2n-1+b2n=-(2n)2+(2n+1)2=4n+1.
则数列{bn}的前n项和T2n=$\frac{n(5+4n+1)}{2}$=2n2+3n.
故答案为:2n2+3n.
点评 本题考查了分组求和、等差数列的求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
13.已知△ABC的三内角A,B,C,所对三边分别为a,b,c,sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,若△ABC的面积S=24,b=10,则a的值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
17.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,A,B分别为双曲线C左、右两支上的点,且四边形ABOF(O为坐标原点)为菱形,则双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
14.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,离心率为$\frac{1}{2}$,倾斜角为$\frac{π}{4}$的动直线l与椭圆E交于M,N两点,则当△FMN的周长的取得最大值8时,直线l的方程为( )
| A. | x-y-1=0 | B. | x-y=0 | C. | x-y-$\sqrt{3}$=0 | D. | x-y-2=0 |
11.双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$(a>0,b>0)与抛物线$y=\frac{1}{8}{x^2}$有一个公共焦点F,双曲线上过点F且垂直于y轴的弦长为$\frac{{2\sqrt{3}}}{3}$,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{3}$ |
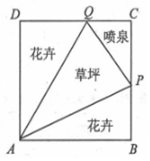 如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.