题目内容
8.已知函数f(x)=|x-a|+|2x-1|.(Ⅰ)当a=1时,解不等式f(x)≥2;
(Ⅱ)求证:$f(x)≥|a-\frac{1}{2}|$.
分析 (I)分类讨论,即可解不等式;
(II)利用绝对值不等式,即可证明.
解答 (Ⅰ)解:当a=1时,不等式f(x)≥2,即|x-1|+|2x-1|≥2.
x<$\frac{1}{2}$时,不等式可化为1-x+1-2x≥2,解得x≤0,∴x≤0;
$\frac{1}{2}≤x≤1$时,不等式可化为1-x+2x-1≥2,解得x≥2,∴x无解;
x>1时,不等式可化为x-1+2x-1≥2,解得x≥$\frac{4}{3}$,∴x≥$\frac{4}{3}$;
综上所述,不等式的解集为(-∞,0]∪[$\frac{4}{3}$,+∞);
(Ⅱ)证明:f(x)=|x-a|+|2x-1|≥|a-x|+|x-$\frac{1}{2}$|≥|a-$\frac{1}{2}$|.
点评 本题考查不等式的解法与证明,考查分类讨论的数学思想,考查绝对值不等式的运用,属于中档题.

练习册系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
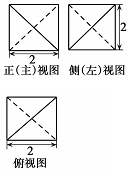

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
16.已知复数z=m+2i,且(2+i)z是纯虚数,则实数m=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
13.已知△ABC的三内角A,B,C,所对三边分别为a,b,c,sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,若△ABC的面积S=24,b=10,则a的值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
17.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,A,B分别为双曲线C左、右两支上的点,且四边形ABOF(O为坐标原点)为菱形,则双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |