题目内容
1.设向量$\overrightarrow a=(1,\sqrt{3}),\overrightarrow b=(m,\sqrt{3})$,且$\overrightarrow a,\overrightarrow b$的夹角为$\frac{π}{3}$,则m=-1.分析 根据平面向量的数量积,列出方程,即可求出m的值.
解答 解:向量$\overrightarrow a=(1,\sqrt{3}),\overrightarrow b=(m,\sqrt{3})$,且$\overrightarrow a,\overrightarrow b$的夹角为$\frac{π}{3}$,
则$|\overrightarrow a|=2,|\overrightarrow b|=\sqrt{{m^2}+3},\overrightarrow a•\overrightarrow b=m+3$,
根据 公式$\overrightarrow a•\overrightarrow b=|\overrightarrow a||\overrightarrow b|cos<\overrightarrow a,\overrightarrow b>$得:
$m+3=2\sqrt{{m^2}+3}×\frac{1}{2}$,
解得m=-1.
故答案为:-1.
点评 本题考查了平面向量的数量积与应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.函数f(x)=lgx+x-2的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,10) |
9.“($\frac{1}{3}$)x<1”是“$\frac{1}{x}$>1”的( )
| A. | 充分且不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
16.已知复数z=m+2i,且(2+i)z是纯虚数,则实数m=( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
13.已知△ABC的三内角A,B,C,所对三边分别为a,b,c,sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,若△ABC的面积S=24,b=10,则a的值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
11.双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$(a>0,b>0)与抛物线$y=\frac{1}{8}{x^2}$有一个公共焦点F,双曲线上过点F且垂直于y轴的弦长为$\frac{{2\sqrt{3}}}{3}$,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{3}$ |
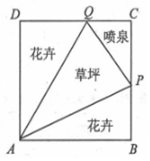 如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.