题目内容
已知抛物线y2=4x的焦点F,A,B是抛物线上横坐标不相等的两点,若AB的垂直平分线与x轴的交点是(4,0),则|AB|是最大值为( )
| A、2 | B、4 | C、6 | D、10 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:依题意知,抛物线y2=4x的焦点F(1,0),设A(x1,y1) B(x2,y2),利用线段的垂直平分线的性质可得,|MA|2=|MB|2,整理可知x1+x2=4,利用不等式AB≤AF+BF即可求得答案.
解答:
解:∵抛物线y2=4x的焦点F(1,0),设A(x1,y1) B(x2,y2),
∵线段AB的垂直平分线恰过点M(4,0),
∴|MA|2=|MB|2,即(4-x1)2+y12=(4-x2)2+y22,
又y12=4x1,y22=4x2,代入并展开得:
16+x12-8x1+4x1=x22-8x2+16+4x2,
即x12-x22=4x1-4x2,又x1≠x2,
x1+x2=4,
∴线段AB中点的横坐标为
(x1+x2)=2,
∴AB≤AF+BF=(x1+
)+(x2+
)=4+2=6(当A,B,F三点共线时取等号).
即|AB|是最大值为6.
故选:C.
∵线段AB的垂直平分线恰过点M(4,0),
∴|MA|2=|MB|2,即(4-x1)2+y12=(4-x2)2+y22,
又y12=4x1,y22=4x2,代入并展开得:
16+x12-8x1+4x1=x22-8x2+16+4x2,
即x12-x22=4x1-4x2,又x1≠x2,
x1+x2=4,
∴线段AB中点的横坐标为
| 1 |
| 2 |
∴AB≤AF+BF=(x1+
| p |
| 2 |
| p |
| 2 |
即|AB|是最大值为6.
故选:C.
点评:本题考查抛物线的简单性质,考查线段的垂直平分线的性质的应用,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
正三棱柱的左视图如图所示,则该正三棱柱的侧面积为( )
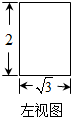

| A、4 | ||||
| B、12 | ||||
C、
| ||||
| D、24 |
已知l,m是两条不同的直线,α是一个平面,且l∥α,则下列命题正确的是( )
| A、若l∥m,则m∥α |
| B、若m∥α,则l∥m |
| C、若l⊥m,则m⊥α |
| D、若m⊥α,则l⊥m |
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )
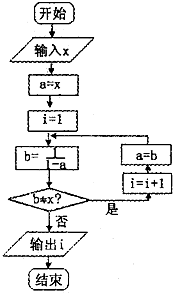

| A、3 | B、5 | C、6 | D、8 |
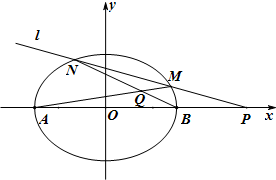 已知椭圆C:
已知椭圆C: