题目内容
某商场的一种商品每件进价为10元，据调查知每日销售量m（件）与销售价x（元）之间的函数关系为m=70-x，10≤x≤70．设该商场日销售这种商品的利润为y（元）．（单件利润=销售单价-进价；日销售利润=单件利润×日销售量）
（1）求函数y=f（x）的解析式；
（2）求该商场销售这种商品的日销售利润的最大值．
（1）求函数y=f（x）的解析式；
（2）求该商场销售这种商品的日销售利润的最大值．
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：（1）用每件的利润乘以销售量得到每天的利润．
（2）由（1）得到的是一个二次函数，利用二次函数的性质，可以求出最大利润以及销售单价．
（2）由（1）得到的是一个二次函数，利用二次函数的性质，可以求出最大利润以及销售单价．
解答：
解：（1）y=m（x-10），
=（x-10）（70-x），
=-x2+80x-700（10≤x≤70）；
（2）∵y=-x2+80x-700=-（x-40）2+900，10≤x≤70，
∴当x=40元时，最大利润y=900元．
=（x-10）（70-x），
=-x2+80x-700（10≤x≤70）；
（2）∵y=-x2+80x-700=-（x-40）2+900，10≤x≤70，
∴当x=40元时，最大利润y=900元．
点评：本题考查了二次函数的应用，根据配方法求出二次函数的顶点坐标是解题关键．
练习册系列答案
相关题目
为了了解某校今年高三男生的身体状况，随机抽查了部分男生，将测得的他们的体重（单位：千克）数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．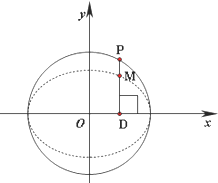
如图，在圆x2+y2=2上任取一点P，过点P作x轴的垂线段PD，D为垂足．点M在线段DP上，且